Tavex koristi kolačiće kako bi osigurao funkcionalnost veb stranice i poboljšao Vaše korisničko iskustvo. Prikupljanje podataka iz kolačića nam pomaže da Vam pružimo najbolje iskustvo, da čuvamo Vaš račun bezbednim i omogućava nam da personalizujemo sadržaj oglasa. Možete saznati više na linku kolačići.
Izaberite koje kolačiće možemo da koristimo
Kolačići su male tekstualne i cifrene datoteke koje se preuzimaju i čuvaju u vašem pregledaču dok posećujete veb stranicu. Mogu da se koriste za praćenje stranica koje posećujete na veb stranici, za čuvanje informacija koje unesete ili za pamćenje vaših preferencija kao što su postavke jezika sve dok posećujete veb stranicu.
Ovde možete da pronađete sve kolačiće koji mogu biti sačuvani u vašem pregledaču dok pretražujete sajt, za šta se koriste i koliko dugo se svaki od njih čuva.
| Naziv kolačića | Opis | Vreme trajanje |
|---|---|---|
| tavex_cookie_consent | ||
| tavex_customer | ||
| wp-wpml_current_language | ||
| AWSALB | ||
| AWSALBCORS | ||
| NO_CACHE | ||
| PHPSESSID | ||
| latest_news | ||
| latest_news_flash | ||
| tavex_recently_viewed_products | ||
| tavex_compare_amount |
| Naziv kolačića | Opis | Vreme trajanje |
|---|---|---|
| chart-widget-tab-*-*-* | ||
| archive_layout |
| Naziv kolačića | Opis | Vreme trajanje |
|---|---|---|
| _ga | ||
| _gid | ||
| _ga_* | ||
| _gac_* | ||
| _gat_gtag_* | ||
| _fbc | ||
| _fbp |
Metode za računanje prinosa investicije

Tabela sadržaja
Na samoj osnovi svake investicije je pretpostavka dobijanja određenog prinosa. Ovo predstavlja nečiji interes za smanjenje njihovog životnog standarda u sadašnjosti, štednjom novca i izdvajanjem za buduće finansijske dobitke.
Ali koje metode treba koristiti za izračunavanje naših dobitaka ili gubitaka? Kako treba da uračunamo sredstva koja ulaze i izlaze iz investicionog portfolija? Koji indikatori prinosa se koriste za upoređivanje performanse portfolija?
U ovom članku ću proći kroz najčešće korišćene metode za izračunavanje prinosa investicija pod različitim okolnostima.
Međutim, želeo bih da naglasim da su za većinu investitora dovoljne prve tri metode. Odeljak sa naprednim metodama je za one koji žele dublje razumevanje kako se njihov investicioni portfolio razvija.
Jednostavan prinos
Najosnovniji način izračunavanja dobiti ili gubitka investicije je korišćenje formule jednostavnog prinosa. Ovo je predstavljeno u obliku procenta. Ovaj procenat pokazuje koliko je neko dobio ili izgubio od investicije.
Formula za jednostavan prinos je:
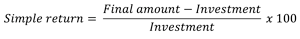
Ova formula važi samo za kratkoročne investicije, i ne uzima u obzir dodatna ulaganja ili likvidaciju (prodaju imovine) tokom perioda ulaganja. Takođe, ova formula ne uzima u obzir sve vrste naknada i provizija koje se plaćaju platformi za trgovanje.
Godišnji prinos
Godišnji prinos pomaže u utvrđivanju koji je godišnji prinos investicije, tokom više godina.
Koja je razlika u odnosu na jednostavan prinos? Činjenica da su prinosi na investicije složeni. To znači da će prinos sledeće godine doći na vrh ovogodišnjeg postojećeg prinosa. Ovogodišnji prinos je na vrhu prošlogodišnjeg prinosa, i tako dalje.
Pošto se iznosi eksponencijalno povećavaju tokom dužeg vremenskog perioda u poređenju sa jednostavnim prinosom, potreban nam je pravilan način izračunavanja godišnjeg prinosa koji se komplikuje tokom investicionog perioda.
Da bismo matematički saznali godišnji prinos investicije, prvo moramo pogledati formulu složene kamate.
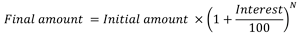
Ako znamo konačni iznos (nakon što je investicija izvršena), početni iznos (šta smo uložili) i za koliko godina (broj perioda N), moramo izračunati kamatnu stopu koja je godišnji prinos.
Izvlačenjem kamatne stope dobijamo:
 Tokom dužeg vremenskog perioda, diversifikovani portfoliji imaju koristi od godišnjeg prinosa između 8% i 12%. Loša strana ove formule, baš kao i u slučaju jednostavnog prinosa, je činjenica da ne uzima u obzir tokove novca u i iz investicionog portfolija.
Tokom dužeg vremenskog perioda, diversifikovani portfoliji imaju koristi od godišnjeg prinosa između 8% i 12%. Loša strana ove formule, baš kao i u slučaju jednostavnog prinosa, je činjenica da ne uzima u obzir tokove novca u i iz investicionog portfolija.
Ukupan prinos
Dve prethodne metode za izračunavanje prinosa investicija imaju za cilj da izraze prinos investicije od rasta cene sredstva. Međutim, ovi prinosi ne uzimaju u obzir dodatne dobitke od investicije.
Ovde govorim o dividendama od akcija. To su takođe prihodi ostvareni istom investicijom, i oni takođe treba da budu uzeti u obzir. Razlika između rasta cena i ukupnog prinosa S&P500 pokazuje veliku razliku koju dividende mogu napraviti.
Da bi se uračunale i dividende, formula koju moramo koristiti je:
![]() Formula je gotovo identična jednostavnom prinosu, ali upravo zato što ova formula želi da pokaže finansijsku dobit tokom čitavog investicionog perioda. Međutim, čak ni formula za ukupni prinos ne računa vađenje i dodavanje novca tokom investicionog perioda (cash flow).
Formula je gotovo identična jednostavnom prinosu, ali upravo zato što ova formula želi da pokaže finansijsku dobit tokom čitavog investicionog perioda. Međutim, čak ni formula za ukupni prinos ne računa vađenje i dodavanje novca tokom investicionog perioda (cash flow).
Neto sadašnja vrednost (NPV)
Tri gore navedene formule su korisne za izračunavanje prinosa investicija nakon što je investicija završena. Ali šta ako želimo da procenimo za koliko vremena će naša investicija početi da donosi profit?
Drugačije rečeno, kada možemo očekivati da zaradimo više od onoga što smo uložili? Da bismo to saznali, moramo izračunati neto sadašnju vrednost (NPV) potencijalne investicije.
Svi smo čuli da jedan evro danas vredi više od jednog evra sutra. To je zbog inflacije i vremenskih preferencija ljudi. Ljudi obično žele stvari sada, jer sada je sigurnije nego godinu dana od sada. To je takođe jedan od razloga zašto mnogi od nas odlučuju da pozajme novac kako bi kupili automobil ili kuću.
Isti koncept važi i za investicije. U poslovanju, vrednost investicije kompanije zavisi od toga koliko i koliko brzo ta investicija može da generiše novac. Da izračunali sadašnju (ili trenutnu) vrednost novca koju ćemo dobiti u budućnosti, moramo uzeti u obzir te prihode u sadašnjem vremenu.
To radimo diskontiranjem budućih novčanih tokova za troškove implementacije tog projekta. Ovaj trošak je predstavljen kao godišnji procenat, što je ponderisani prosek cene kapitala i duga akcionara koji se koristi za tu investiciju.
Formula izgleda ovako:
![]()
N je broj godina. Ovo pomaže u utvrđivanju koja je vrednost novca primljenog u budućnosti danas. Ovi novčani tokovi moraju biti veći od početne investicije, tokom investicionog perioda, kako bi se osiguralo da investicija vredi više od uloženog iznosa.
Ako je NPV negativan, to znači da imamo stvarni gubitak, a sredstva treba da preraspodelimo na projekte sa većim prinosima. NPV nam pokazuje u šta ne treba ulagati.
Napredni načini izračunavanja prinosa investicija
Za nekoga ko je zainteresovan samo za brzo saznanje koliko je profita ostvareno od investicije, gore pomenute formule su dovoljne. Međutim, za naprednije investitore, postoji više formula koje se mogu koristiti.
Kao što ću navesti još četiri u nastavku, takođe ću objasniti koje su njihove prednosti. To uglavnom zavisi od interesa investitora prema onome što on ili ona želi da sazna.
Interna stopa prinosa (IRR)
Interna stopa prinosa je povezana sa neto sadašnjom vrednošću. Njegova formula je izvedena iz NPV-a. IRR procenjuje koliko brzo investitor može da vrati svoju investiciju, uzimajući u obzir vremensku vrednost novca. Izražava se kao prosečna godišnja stopa prinosa.
Da bismo pronašli IRR, moramo izjednačiti formulu NPV sa nulom.
Dakle, formula bi izgledala ovako:
![]()
Kao što vidite, „trošak“ iz imenitelja je zamenjen IRR-om. Rešavanjem ove jednačine možemo pronaći maksimalni godišnji prinos investicije. Međutim, IRR se može izračunati i pomoću tabele (Excel ili Google Sheets), unosom formule „= IRR“ i popunjavanjem zagrada sa ispravnim podacima.
Većinu vremena, IRR se koristi kao način da se predvide investicione odluke. Takođe može pomoći u proceni prinosa uloženog kapitala u različitim investicijama, napravljenih u tačnim vremenskim intervalima.
Međutim, IRR ima dva glavna ograničenja. Prvo, investicije moraju biti izvršene u tačnim vremenskim intervalima. Drugo, mogu postojati samo pozitivni novčani tokovi, što znači da više ne izdvajamo za tu investiciju iz našeg džepa.
Novčano ponderisana stopa prinosa (MWRR ili XIRR)
Money weighted rate of return uzima u obzir protok novca u oba smera. Stoga, ako ste aktivni investitor, najverovatnije ćete koristiti ovaj indikator da biste saznali godišnji prinos vašeg portfolija.
MWRR pokazuje prinosa portfolija uzimajući u obzir instance kada je investitor uložio ili povukao sredstva iz portfelja. Ovaj indikator može biti veoma koristan u pokazivanju posledica pogrešnog tajminga na tržištu.
Da bi se izračunao MWRR, lakše je koristiti tabelu (opet, Excel ili Google Sheets). Formula koja se koristi je „= XIRR“, nakon čega slede tačke podataka za novčane tokove i određene datume.
Vremenski ponderisana stopa prinosa (TWRR)
TWRR se fokusira isključivo na performanse portfolija, bez uzimanja u obzir novčane tokove. Ovaj indikator se najviše koristi za poređenje performansa različitih portfolija od strane menadžera fondova i ETF-ova.
Da bih izračunao TWRR, proći ću kroz jednostavan primer kako bi korake bilo lako razumeti.
Zamislimo da je neko kupio jednu akciju u SPY ETF-u, koji prati S&P500, kojim upravlja State Street, 3. januara 2023. godine po ceni od 380 dolara. 27. jula, indeks je dostigao maksimum od 455 dolara po akciji, tako da je investitor kupio još jednu akciju. Kakav je bio prinos investitora između 1. januara i 29. decembra 2023. godine, ako je 29. decembra jedna akcija SPI koštala 475 dolara?
Prvo, moramo da konstatujemo vremenske periode.
Dakle, imamo:
- 3. januar – 27. jul
- 27. jul – 29. decembar
Sada moramo da izračunamo jednostavne prinose za svaki od ovih perioda:

Sada kada imamo osnovni prinos, moramo da saznamo ceo prinos portfolija tokom 2023. godine. To radimo geometrijskim povezivanjem prinosa.
Formula je sledeća:
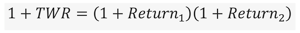
Nakon proračuna, TWRR je jednak 25%. Ali šta smo zapravo izračunali? Pa, ako izračunamo jednostavan prinos cene akcija, dobijamo tačno 25%. Dakle, TWRR, kao što je gore navedeno, pomaže u izračunavanju striktno performansi portfelja, bez uzimanja u obzir novčanih tokova.
Poređenja radi, MWRR ovog primera je 7,78%. Budući da je niži od prinosa samog portfolija, to pokazuje da investitor nije doneo najbolju odluku u ulaganju na vrhuncu tržišta.
Šarpov odnos
Poslednji metod za izračunavanje prinosa sa naše liste je Sharpe ratio. Ovaj metod poredi prinos investicije u odnosu na to koliko je rizična investicija. To može biti veoma koristan pokazatelj prilikom merenja rizika i prinosa različitih investicionih odluka.
Rizik je volatilnost portfolija. Koliko vrednost portfolija odstupa od prosečne cene. Ovo se može izračunati pomoću formule „= STDEV“ u tabeli. Nakon što dobijemo ovu vrednost, moramo izračunati jednostavan prinos investicije i oduzeti stopu bez rizika. Stopa bez rizika je obično prinos kratkoročnih državnih obveznica. Pogledajmo primer.
Indeks S&P500 imao je jednostavan prinos od 24,22% u 2023. godini. Volatilnost indeksa, koristeći Excel, pokazuje odstupanje od 39,17%. Prinos jednogodišnje američke državne obveznice bio je oko 5%.
Sharpeov odnos je:
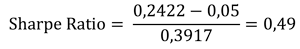
Ovaj 0,49 nam pokazuje niske performanse S&P500 u odnosu na to koliko je nestabilan indeks bio u 2023. Uglavnom, kada Šarpov odnos ima vrednost iznad 1 smatra se dobrom investicionom odlukom.
Zakljuиak
Želeo bih da čestitam svima koji su stigli do kraja članka. Počeli smo sa jednostavnim metodama za izračunavanje naših profita i gubitaka, a završili smo sa prinosom uzimajući u obzir rizik i vremensku vrednost novca.
Želeo bih da naglasim činjenicu da skoro nijedan početni ili manji investitor ne treba da koristi ove formule. Trgovinske platforme već su implementirale načine da pokažu prinos investitora.
Idealno je da stvari budu jednostavne, inače ceo proces ulaganja može uplašiti ljude. A to je veoma nepoželjno, jer samo ulaganjem u imovinu možemo povećati naše bogatstvo.


















